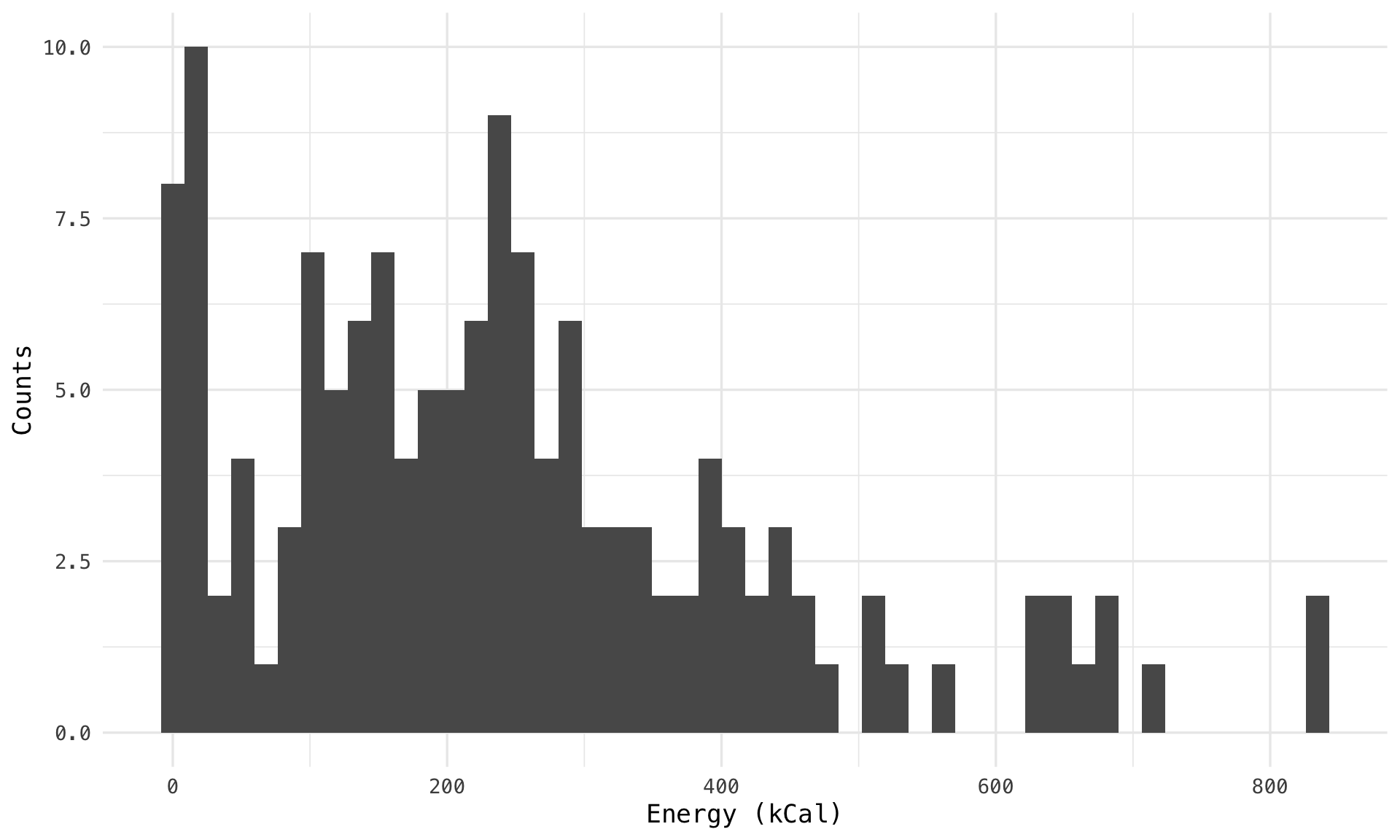
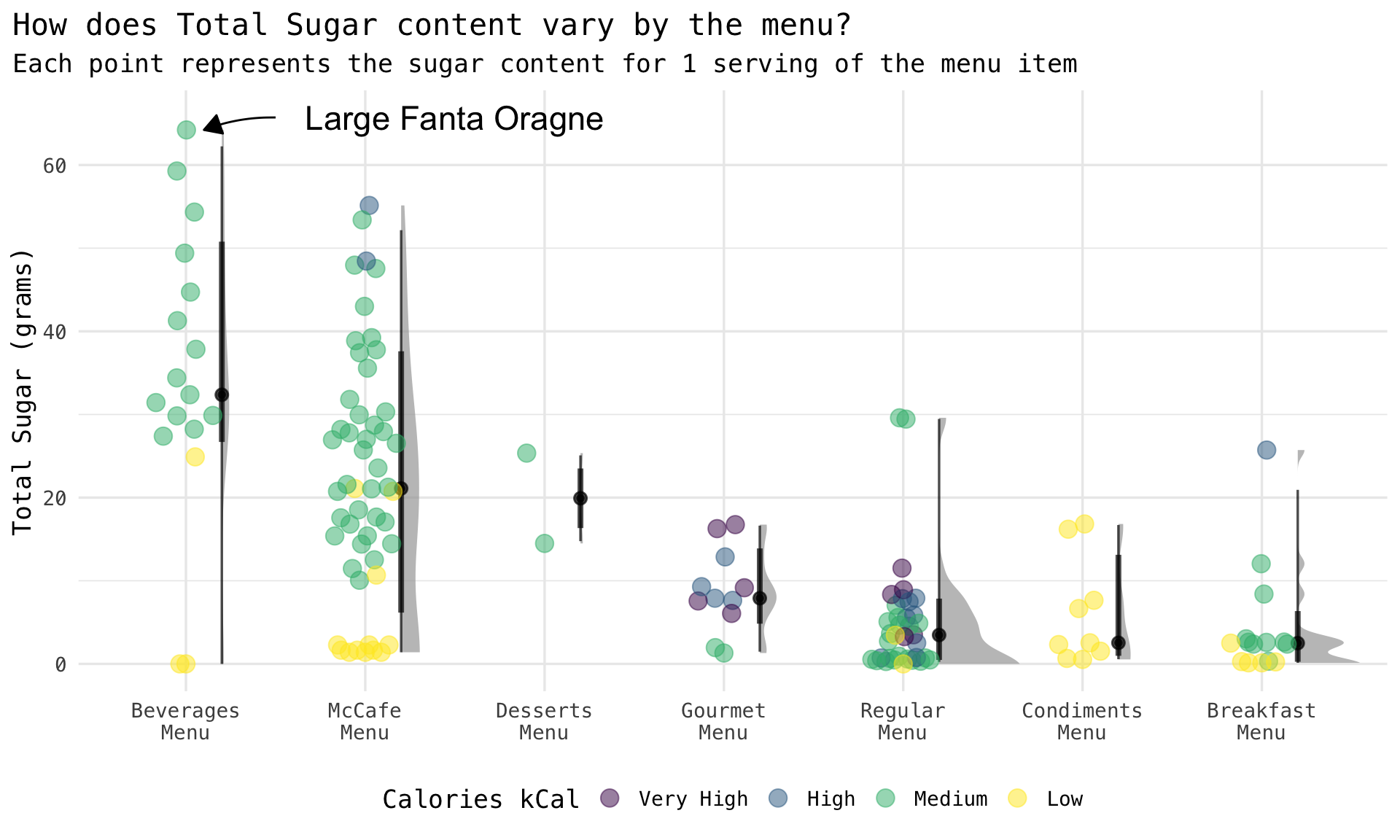
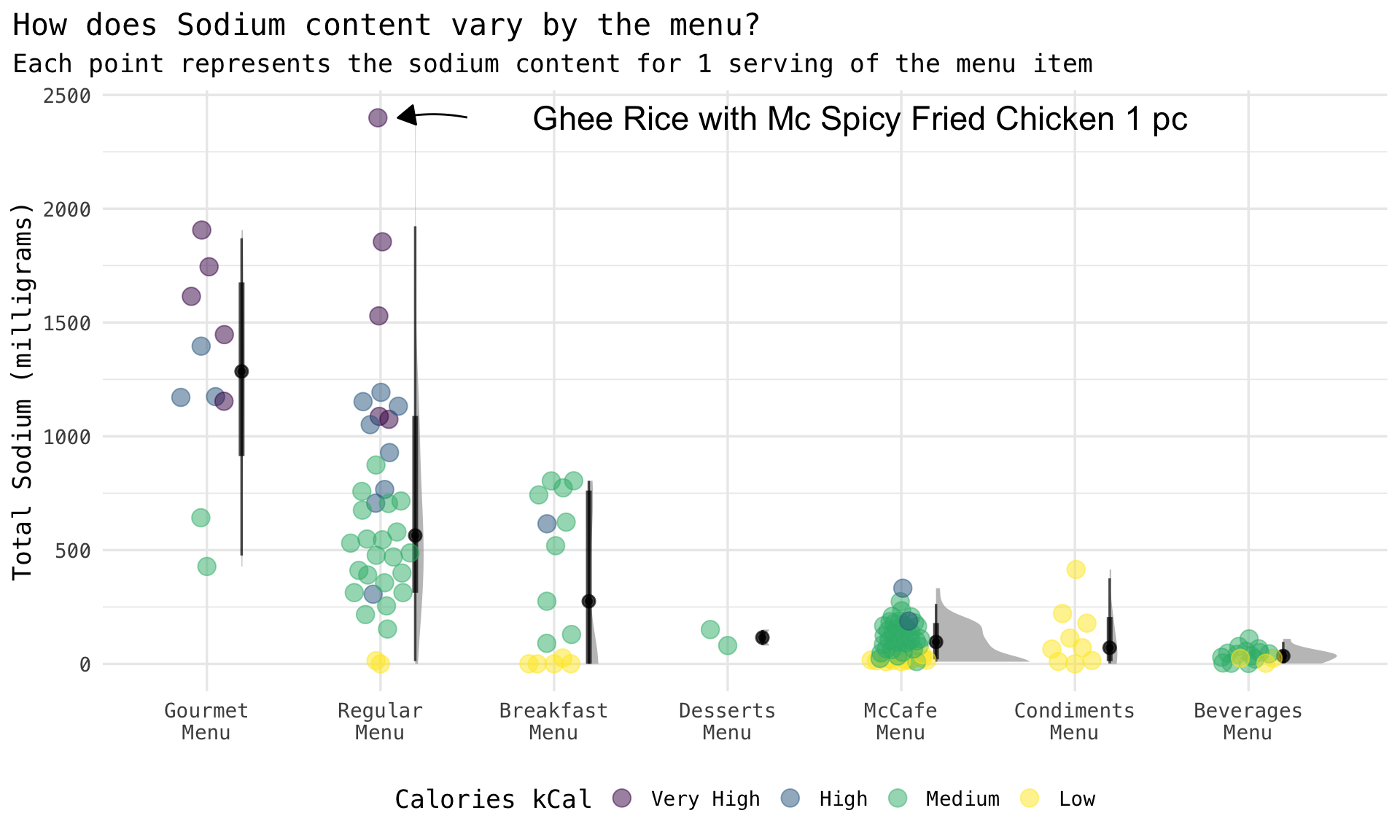
Rows: 141
Columns: 13
$ menu_category <chr> "Regular Menu", "Regular Menu", "Regular Menu", "Regular Menu", "Regu…
$ menu_items <chr> "McVeggie™ Burger", "McAloo Tikki Burger®", "McSpicy™ Paneer Burger",…
$ per_serve_size <chr> "168 g", "146 g", "199 g", "250 g", "177 g", "306 g", "132 g", "87 g"…
$ energy_k_cal <dbl> 402.05, 339.52, 652.76, 674.68, 512.17, 832.67, 356.09, 228.21, 400.8…
$ protein_g <dbl> 10.24, 8.50, 20.29, 20.96, 15.30, 24.17, 7.91, 5.45, 15.66, 15.44, 21…
$ total_fat_g <dbl> 13.83, 11.31, 39.45, 39.10, 23.45, 37.94, 15.08, 11.44, 15.70, 14.16,…
$ sat_fat_g <dbl> 5.34, 4.27, 17.12, 19.73, 10.51, 16.83, 6.11, 5.72, 5.47, 5.79, 7.63,…
$ trans_fat_g <dbl> 0.16, 0.20, 0.18, 0.26, 0.17, 0.28, 0.24, 0.09, 0.16, 0.21, 0.18, 0.2…
$ cholesterols_mg <dbl> 2.49, 1.47, 21.85, 40.93, 25.24, 36.19, 9.45, 5.17, 31.17, 32.83, 66.…
$ total_carbohydrate_g <dbl> 56.54, 50.27, 52.33, 59.27, 56.96, 93.84, 46.36, 24.79, 47.98, 38.85,…
$ total_sugars_g <dbl> 7.90, 7.05, 8.35, 3.50, 7.85, 11.52, 4.53, 2.73, 5.53, 5.58, 5.88, 2.…
$ added_sugars_g <dbl> 4.49, 4.07, 5.27, 1.08, 4.76, 6.92, 1.15, 0.35, 4.49, 3.54, 4.49, 1.0…
$ sodium_mg <dbl> 706.13, 545.34, 1074.58, 1087.46, 1051.24, 1529.22, 579.60, 390.74, 7…