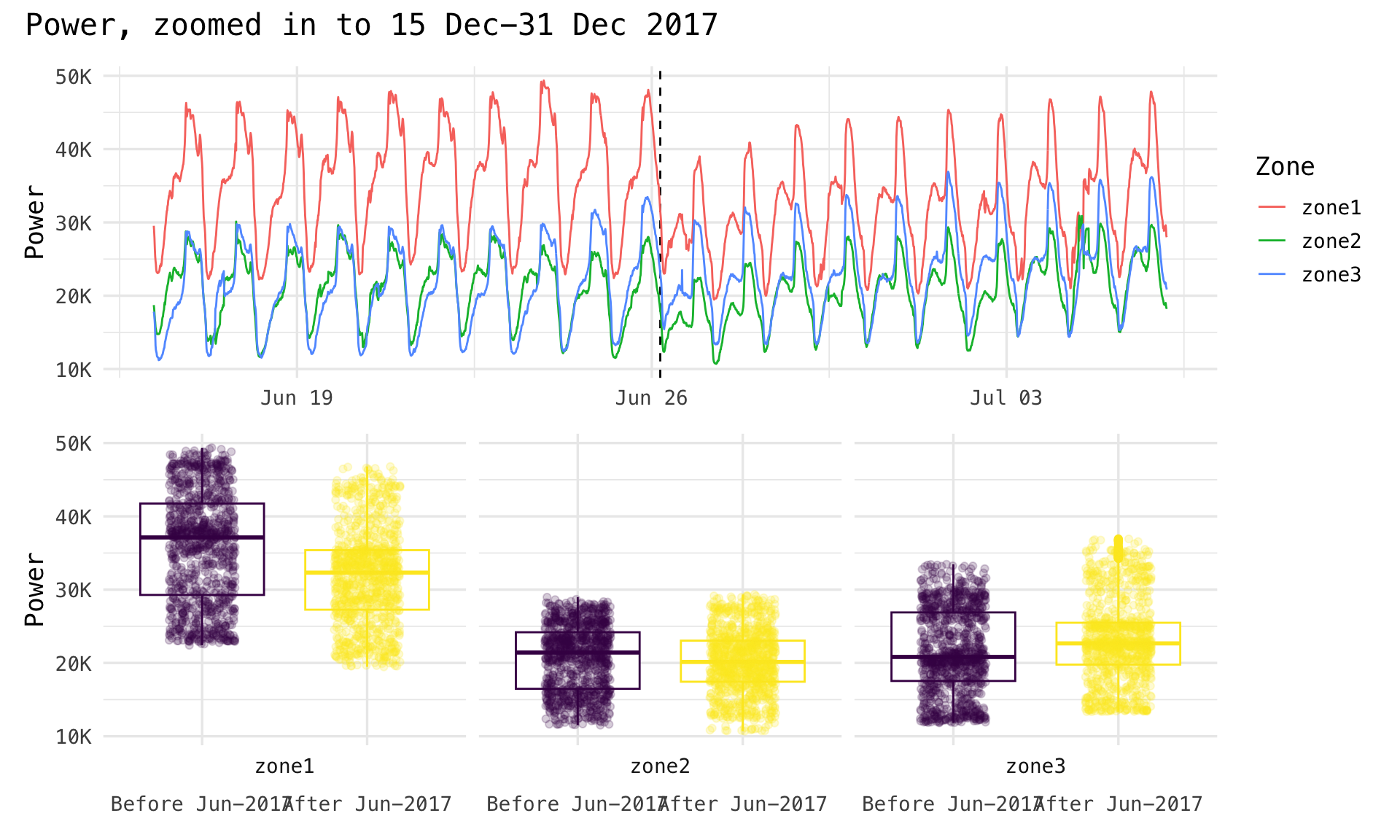
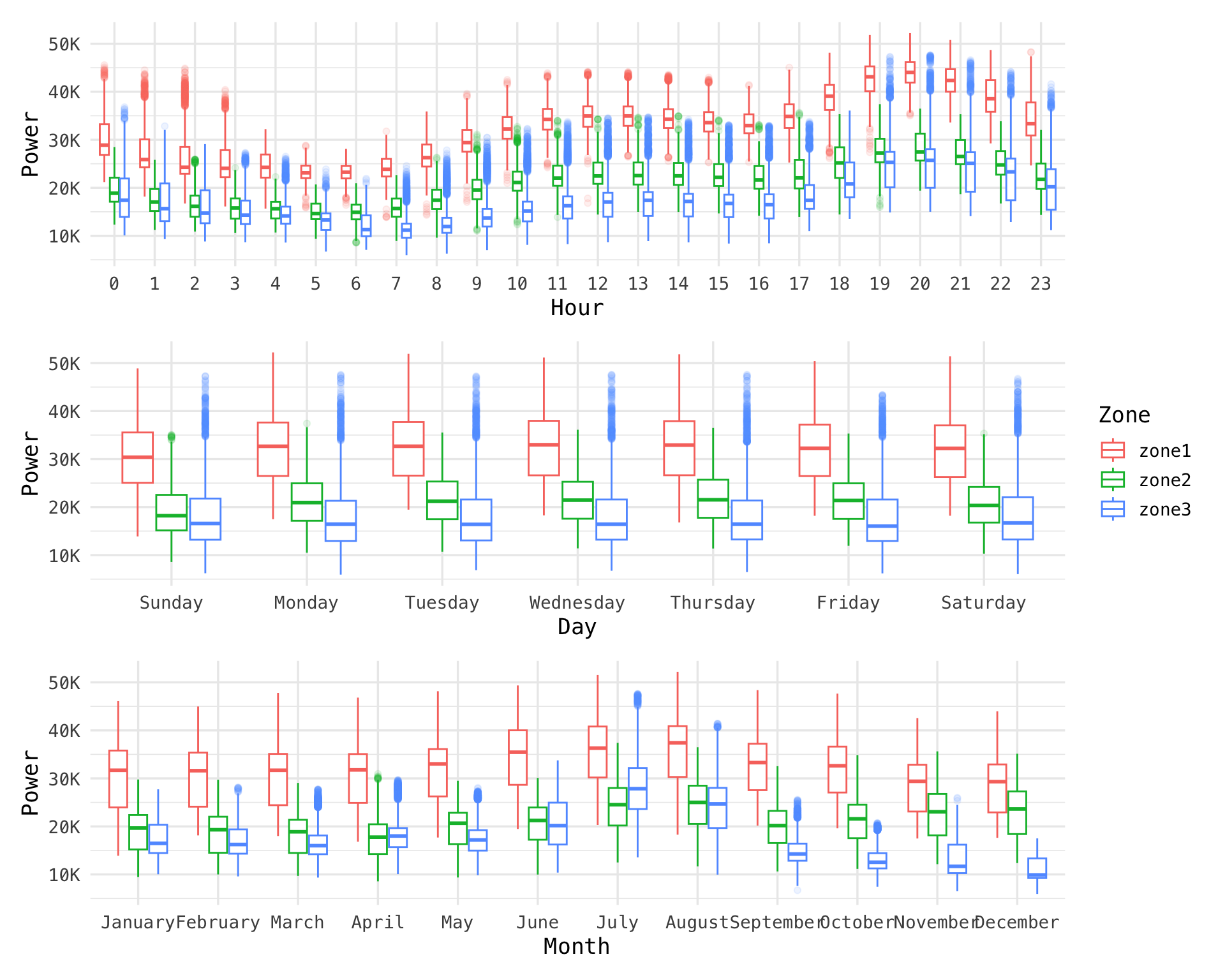
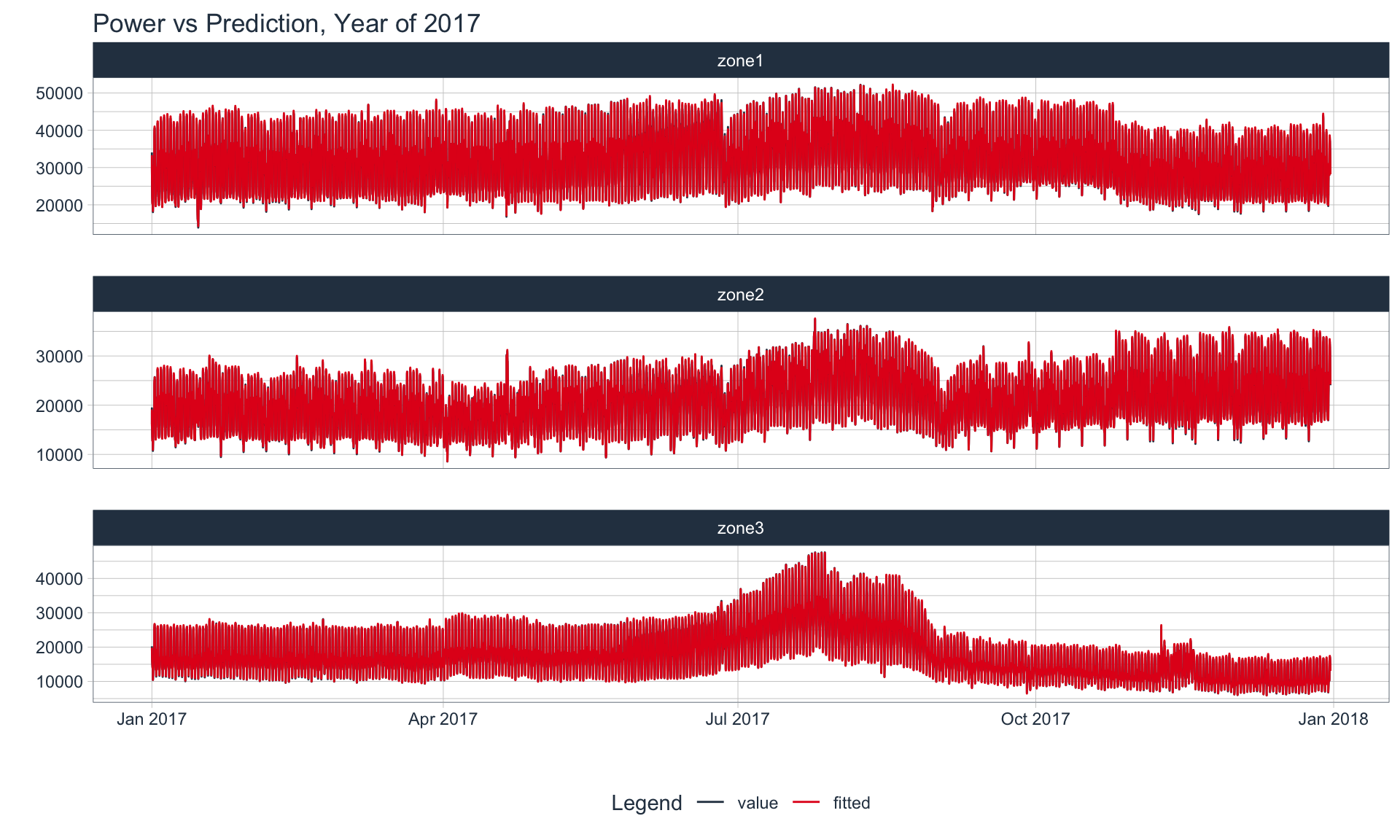
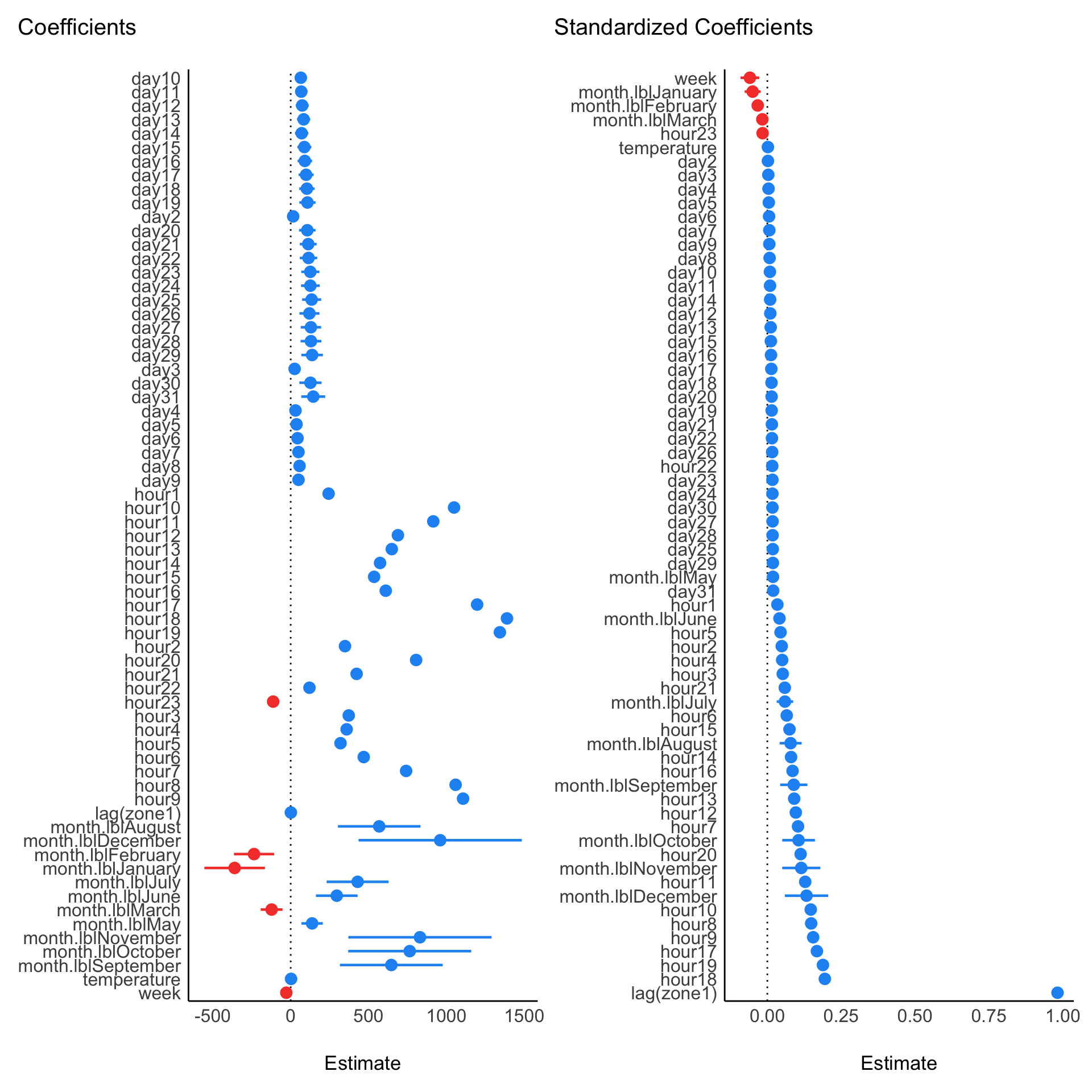
Rows: 52,416
Columns: 24
$ datetime <dttm> 2017-01-01 00:00:00, 2017-01-01 00:10:00, 2017-…
$ temperature <dbl> 6.559, 6.414, 6.313, 6.121, 5.921, 5.853, 5.641,…
$ humidity <dbl> 73.8, 74.5, 74.5, 75.0, 75.7, 76.9, 77.7, 78.2, …
$ wind_speed <dbl> 0.083, 0.083, 0.080, 0.083, 0.081, 0.081, 0.080,…
$ general_diffuse_flows <dbl> 0.051, 0.070, 0.062, 0.091, 0.048, 0.059, 0.048,…
$ diffuse_flows <dbl> 0.119, 0.085, 0.100, 0.096, 0.085, 0.108, 0.096,…
$ zone1 <dbl> 34055.70, 29814.68, 29128.10, 28228.86, 27335.70…
$ zone2 <dbl> 16128.88, 19375.08, 19006.69, 18361.09, 17872.34…
$ zone3 <dbl> 20240.96, 20131.08, 19668.43, 18899.28, 18442.41…
$ dt_hr <dttm> 2017-01-01 00:00:00, 2017-01-01 00:00:00, 2017-…
$ year <int> 2017, 2017, 2017, 2017, 2017, 2017, 2017, 2017, …
$ half <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ quarter <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ month <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ month.lbl <ord> January, January, January, January, January, Jan…
$ day <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ hour <ord> 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, …
$ wday <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ wday.lbl <ord> Sunday, Sunday, Sunday, Sunday, Sunday, Sunday, …
$ mday <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ qday <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ yday <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …
$ mweek <int> 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, …
$ week <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, …